Matrix ~ Wolfram MathWorld

http://mathworld.wolfram.com/Matrix.html

A matrix is a concise and useful way of uniquely representing and working with linear transformations. In particular, every linear transformation can be represented by a matrix, and every matrix corresponds to a unique linear transformation. The matrix, and its close relative the determinant, are extremely important concepts in linear algebra, and were first formulated by Sylvester (1851) and Cayley.

In his 1851 paper, Sylvester wrote, "For this purpose we must commence, not with a square, but with an oblong arrangement of terms consisting, suppose, of 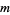lines and 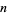columns. This will not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants by fixing upon a number 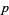, and selecting at will 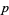lines and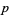 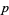th order." Because Sylvester was interested in the determinant formed from the rectangular array of number and not the array itself (Kline 1990, p. 804), Sylvester used the term "matrix" in its conventional usage to mean "the place from which something else originates" (Katz 1993). Sylvester (1851) subsequently used the term matrix informally, stating "Form the rectangular matrix consisting of 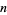rows and 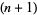columns.... Then all the 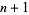columns, the squares corresponding of determinants that can be formed by rejecting any one column at pleasure out of this matrix are identically zero." However, it remained up to Sylvester's collaborator Cayley to use the terminology in its modern form in papers of 1855 and 1858 (Katz 1993).

In his 1867 treatise on determinants, C. L. Dodgson (Lewis Carroll) objected to the use of the term "matrix," stating, "I am aware that the word 'Matrix' is already in use to express the very meaning for which I use the word 'Block'; but surely the former word means rather the mould, or form, into which algebraical quantities may be introduced, than an actual assemblage of such quantities...." However, Dodgson's objections have passed unheeded and the term "matrix" has stuck.

The transformation given by the system of equations

			(1)
			(2)
			(3)
			(4)

is represented as a matrix equation by

(5)

where the 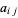are called matrix elements.

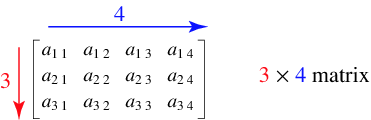
An matrix consists of rows and columns, and the set of matrices with real coefficients is sometimes denoted . To remember which index refers to which direction, identify the indices of the last (i.e., lower right) term, so the indices of the last element in the above matrix identifies it as an matrix.

A matrix is said to be square if , and rectangular if . An matrix is called a column vector, and a matrix is called a row vector. Special types of square matrices include the identity matrix , with (where is the Kronecker delta) and the diagonal matrix (where are a set of constants).

In this work, matrices are represented using square brackets as delimiters, but in the general literature, they are more commonly delimited using parentheses. This latter convention introduces the unfortunate notational ambiguity between matrices of the form and the binomial coefficient

(6)

When referenced symbolically in this work, matrices are denoted in a sans serif font, e.g, 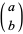, , 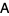etc. In this concise notation, the transformation given in equation (5) can be written

(7)

where and are vectors and is a matrix. A number of other notational conventions also exist, with some authors preferring an italic typeface.

It is sometimes convenient to represent an entire matrix in terms of its matrix elements. Therefore, the th element of the matrix could be written , and the matrix composed of entries could be written as , or simply for short.

Two matrices may be added (matrix addition) or multiplied (matrix multiplication) together to yield a new matrix. Other common operations on a single matrix are matrix diagonalization, matrix inversion, and transposition.

The determinant 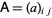or 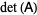of a matrix 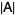is a very important quantity which appears in many diverse applications. The sum of the diagonal elements of a square matrix is known as the matrix trace 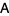and is also an important quantity in many sorts of computations.

SEE ALSO: Adjacency Matrix, Adjugate Matrix, Alternating Sign Matrix, Antisymmetric Matrix, Block Matrix, Bohr Matrix, Bourque-Ligh Conjecture, Cartan Matrix, Circulant Matrix, Condition Number, Cramer's Rule, Determinant, Diagonal Matrix, Dirac Matrices, Eigenvector, Elementary Matrix, Elementary Row and Column Operations, Equivalent Matrix, Fourier Matrix, Gram Matrix, Hilbert Matrix, Hypermatrix, Identity Matrix, Ill-Conditioned Matrix, Incidence Matrix, Irreducible Matrix, Kac Matrix, Least Common Multiple Matrix, LU Decomposition, Markov Matrix, Matrix Addition, Matrix Decomposition Theorem, Matrix Inverse, Matrix Multiplication, Matrix Trace, McCoy's Theorem, Minimal Matrix, Normal Matrix, Pauli Matrices, Permutation Matrix, Positive Definite Matrix, Random Matrix, Rational Canonical Form, Reducible Matrix, Roth's Removal Rule, Shear Matrix, Singular Matrix, Smith Normal Form, Sparse Matrix, Special Matrix, Square Matrix, Stochastic Matrix, Submatrix, Symmetric Matrix, Tournament Matrix

REFERENCES:

Arfken, G. "Matrices." §4.2 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 176-191, 1985.

Bapat, R. B. Linear Algebra and Linear Models, 2nd ed. New York: Springer-Verlag, 2000.

Dodgson, C. L. An Elementary Treatise on Determinants, with Their Application to Simultaneous Linear Equations and Algebraical Geometry. London: Macmillan, 1867.

Frazer, R. A.; Duncan, W. J.; and Collar, A. R. Elementary Matrices and Some Applications to Dynamics and Differential Equations. Cambridge, England: Cambridge University Press, 1955.

Katz, V. J. A History of Mathematics. An Introduction. New York: HarperCollins, 1993.

Kline, M. Mathematical Thought from Ancient to Modern Times. Oxford, England: Oxford University Press, 1990.

Lütkepohl, H. Handbook of Matrices. New York: Wiley, 1996.

Meyer, C. D. Matrix Analysis and Applied Linear Algebra. Philadelphia, PA: SIAM, 2000.

Sylvester, J. J. "Additions to the Articles 'On a New Class of Theorems' and 'On Pascal's Theorem.' " Philos. Mag., 363-370, 1850. Reprinted in J. J. Sylvester's Mathematical Papers, Vol. 1. Cambridge, England: At the University Press, pp. 145-151, 1904.

Sylvester, J. J. An Essay on Canonical Forms, Supplement to a Sketch of a Memoir on Elimination, Transformation and Canonical Forms. London, 1851. Reprinted in J. J. Sylvester's Collected Mathematical Papers, Vol. 1. Cambridge, England: At the University Press, p. 209, 1904.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.

Zhang, F. Matrix Theory: Basic Results and Techniques. New York: Springer-Verlag, 1999.

CITE THIS AS:

Weisstein, Eric W. "Matrix." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Matrix.html

++++++++++++++++++++++++++++++++++++
HumanE-Liberation-Party Blog
http://help-matrix.blogspot.com/
++++++++++++++++++++++++++++++++++++